Novocherkassk Engineering and Reclamation Institute named after A.K. Kortunova
Russian Federation
Russian Federation
from 01.01.2010 to 01.01.2019
Novocherkassk, Rostov-on-Don, Russian Federation
One of the quality indicators of scientific research is the availability of statistical processing of research results obtained as a result of laying test plots in forestry production. The primary task for a researcher (forestry engineer) is to prove the reliability of the results. Great opportunities for statistical calculations for researchers are opened using the Mathcad application package (Mathcad AP). The purpose of the work is a detailed description and presentation of the mathematical and statistical processing of inventory data obtained as a result of laying the test plot and measuring trees of the Norway maple (Acer platanoides L.) along the Shakhtinsky highway, highway 60N-248. The research methodology consists in the fact that, using the Mathcad AP, specific examples provide step-by-step actions and calculations to obtain the main statistical indicators. A taxation indicator of the diameter at a height of 1.3 m of the maple trees (Acer platanoides L.) has been processed. The main results of the study are: a sample average diameter is 27.1 cm; the variability of the diameter is characterized by such indicators as a standard deviation of 9.6 cm and a coefficient of variation of 35.3%. They indicate significant variability of the studied trait. The reliability assessment leads to the conclusion that the reliability of the sample average, standard deviation, coefficient of variation, and asymmetry keeps at 5% level of significance. The main findings of the study show that the Mathcad AP enables to operate with a large number of data, to process them quickly and with sufficient accuracy, and compare the results of the obtained measurements during complete enumeration in forestry.
mathematical and statistical processing, sylvicultural research, statistical data processing, reliability of research results, Mathcad application package (Mathcad AP).
Введение. Основные области исследований в соответствии с паспортом специальности 06.03.01 «Лесные культуры, селекция, семеноводство»– это изучение плодоношения, лесоводственно-таксационная оценка чистых и смешанных искусственных насаждений(закладка пробных площадей на которых определяются основные параметры, например, высота и диаметры деревьев, освещенность под пологом насаждения, текущие приросты), применение удобрений в питомниках и на лесокультурных площадях, а также другие вопросы[3,13].
Одним из показателей добротности научных исследований является наличие статистической обработки данных (результатов исследований), полученных в результате закладки пробных площадей, а первостепенной задачей для исследователя является доказательство факта достоверности полученных результатов.Зачастую, исследователи, проводя эксперимент, видят показатели, которые на первый взгляд предвещают значимые выводы[10,19].Например, Кружилин С.Н., при проведении статистической обработки заметил, что высотадуба черешчатогов лесных культурахНижнего Дона, созданных с применением разных типов смешения,в условиях сухих дубрав разнотравно-злаковой степи является не достоверной, хотя на первый взгляд она заметно больше чем у дуба, произрастающего в сухой степи [10].
В книге «Энциклопедия археологии» (Дебора М. Пирсолл, 2008)описываются способы, позволяющие избежать неправильного толкования статистических данных, включающие в себя использование надлежащей схемы и исключение предвзятости при проведении исследований [17].
Неправильное использование статистических данных может быть, как случайным, так и преднамеренным, Д.Хафф (1954) в своей книге «Как лгать при помощи статистики» излагаетряд соображений по поводу использования и неправильного применения статистических данных.В статье «Статистические методы, используемые в журналах по высшему образованию с 2006 по 2010 года» (Р. Варн, М. Лазо, Т. Рамос, и Н. Риттер,2012)[18], анализу подлежат статьи из различных журналов,проводится обзор статистических методов, используемых в определённых областях науки, в итоге авторы приходят к выводу, чтостатистические данныедолжны быть достоверны, а не должны выглядеть идеально.
Основными авторами, доступно охарактеризовавшими методики математико-статистической обработки материалов применительно к лесохозяйственным исследованиям, являются: Митропольский А.К., 1971 [12]; Зайцев Г.Н., 1984 [5]; Доспехов Б.А. [3]; Ивонин В.М., Пеньковский Н.Д., 2003 [6], Колмогоров А.Н., 2005 («Избранные труды. В 6-ти томах. Том 2. Теория вероятностей и математическая статистика»); Барышникова Е.В., 2010 [1];Танюкевич В.В., 2004, 2011 [14]; ХуснутдиновР.Ш., 2014 («Сборник задач по теории вероятности и математической статистике. Учебное пособие»), Гмурман В.Е., 2003, 2017 [2]. Например, Доспеховым Б.А. даны основы статистической обработки результатов исследований и техника математической обработки данных наблюдений, однофакторных и многофакторных полевых и вегетационных опытов [3].Ивониным В.М. и Пеньковским Н.Д.показано вычисление основных параметров статистического ряда[6]. Гмурман В.Е. большое внимание уделил статистическим методам обработки экспериментальных данных [2].
К сожалению, авторы не дают конкретные рекомендации по программному обеспечению, способному с максимальной точностью обработать результаты лесокультурных исследований, поэтомуостаются не раскрытыми вопросы в какой программе всё-таки рассчитать и сравнить результаты, полученные при подеревной инвентаризации.Нами сделана попытка с помощью пакета прикладных программMathcad(далеепо тексту – ППП Mathcad) на конкретных примерах пошагово представить действия и расчёты для получения основных статистических показателей, применительно к лесокультурным исследованиям, в чём и состоит научная новизна представленной работы.
Материалы и методы исследования. Во многих диссертационных работах в разделе «Методика проведения исследований» встречаются записи: результаты полученных измерений подвергались математической обработке на персональном компьютере с использованием пакетов прикладных программ «Statgraphics», «Biostat», «MicrosoftExcel» [11];математико-статистическая обработка материалов производилась с помощью программ STATGRAPHICS и Excel для среды MS Windows [8];для оценки достаточности количества наблюдений и достоверности полученных результатов проводилась математическая обработка, рассчитывали: М±mм, коэффициент вариации (±С,%), точность опыта (±Р,%)[10].Такие общие характеристики на фоне детализации других специализированных методик говорят о том, что у исследователей не возникает проблем с математико-статистической обработкой материалов, что статистика выполнена «общепринятыми в математике методами». Важным моментом для исследователя является понимание полученных параметров статистических показателей, уметь пользоваться ими и анализировать их. Главными недостатками,которые представляются очевидными, при обработкеполевых исследований являются:анализ большого объёма обрабатываемой информации, который требует значительные временные затраты; также при обработке данных с помощью математических методов возрастает вероятность возникновения ошибки, на устранение которой потребуется дополнительное время. Всевышеуказанные трудности имеют место приобработке данных, полученных в результате закладки пробной площади и подеревной инвентаризации и в этой связи представляется необходимойавтоматизация процесса.Отсюда и применение специализированных программ и интернет-сайтов в которых гораздо проще провести расчёт статистики. Большие возможности статистических расчётов для исследователей открываются при помощи пакета прикладных программ Mathcad (ППП Mathcad). Mathcad – это уникальный математический пакет для работы с уравнениями, числами, текстом и графиками [9]. При этом, важно отметить, что все вычисления в ППП Mathcad производятся автоматически, т.е. изменив исходные данные, мы мгновенно получаем вычисленные показатели для введённой выборки. Формулы в ППП Mathcad, в отличие от, например, программы для работы с электронными таблицами MicrosoftExcel, выглядят также, как и в учебнике по статистической обработке, что позволяет вставлять фрагменты формул, графиков и вычислений (расчётов), созданных в ППП Mathcadв текстовый редактор MicrosoftWord.
В данной работе использованы методики: подеревной инвентаризации, пробные площади заложены с учётом ОСТ 56-69-83 «Площади пробные лесоустроительные. Методы закладки»; ГОСТ 16483.6-80 (СТ СЭВ 1141-78) [3], а также различные статистические методы (аналитических группировок, индексный и структурный анализы) [5].
Целью представленной работы является детальное описание и представление математико-статистической обработки данных, полученных в результате закладки пробной площади и подеревной инвентаризации в г. Новочеркасске, с использованием ППП Mathcad[1,9], применительно к таксационному показателю –диаметр на высоте
Для выполнения поставленной цели работы нам необходимо было выполнить следующие задачис использованием ППП Mathcad:
а) записать данные, полученные в результате полевого обследования деревьев в ППП Mathcad.
б) провести первичную обработку данных наблюдения (диаметра) и построить статистическое распределение выборки с помощью встроенных функций ППП Mathcad.
в) построить полигон и гистограмму теоретической кривой нормального распределения диаметра клёна остролистного (Acerplatanoides L.) на высоте 1,3 м. Выдвинуть гипотезу о законе распределения исследуемой случайной величины по виду гистограммы (или полигона).
г) вычислить основные статистические показатели, такие как выборочная средняя, выборочная дисперсия, среднее квадратическое отклонение, коэффициент вариации, асимметрию и эксцесс с помощью ППП Mathcad.
д) найти ошибки полученных показателей и относительную ошибку выборочной средней. Пользуясь критерием Стьюдента, определить достоверность статистических показателей для 5% - ного уровня значимости.
е) при уровне значимости α = 0,05, проверить по критерию Пирсона гипотезу о нормальном распределении генеральной совокупности.
ж) вычислить доверительные интервалы для генерального среднего, для коэффициента вариации и среднего квадратического отклонения в генеральной совокупности.
з) провести анализ результатов полученных данныхс использованием ППП Mathcadматематико-статистической обработки результатов лесокультурных исследований.
В соответствии с методикой исследования [3] полевой обмер деревьев был проведён 9 и 10 октября 2017 года. Объектом исследований являлись деревья тополя пирамидального (Populuspyramidalis L.) [16]и клёна остролистного (AcerplatanoidesL.) [16], произрастающие по обеим сторонам Шахтинского шоссе, трасса 60Н-248. Исследуемая территория ограничена северным выездом из г. Новочеркасска и южным въездом п. ПерсиановскийОктябрьского района Ростовской области, протяжённость участка составляет
Рядовая посадка тополя, с примесью деревьев клёна располагается в западной части от автомагистрали, а посадка клёна на противоположной стороне от автомагистрали, в восточной части (рисунок 1).
На рисунке 2 показаны тополь пирамидальный и клён остролистный на объекте исследований, произрастающие деревья выполняют функцию придорожных насаждений. Насаждения, которые формируют придорожную полосу имеют возраст 60-65 лет.
На пробной площади при подеревной инвентаризации были проведены измерения высоты деревьев (h, м), диаметра на высоте
Все этапы математико-статистической обработки результатов, полученных при инвентаризации, расчёт основных статистических показателей и их оценка проведены с использованием ППП Mathcad [1,3], применительно к таксационному показателю (диаметр на высоте
Необходимые для расчётов в ППП Mathcad данные отражены в таблице 1.
Результаты исследования и их обсуждение. Анализируя таблицу 1, выборочная совокупность является большой выборкой, так как содержит результаты 100 наблюдений (измерений), среди значений также встречаются повторяющиеся варианты. Полученные экспериментальные данные необходимо обработать интервальным методом.

|
С |
Рис. 1. Ситуационная схема месторасположения объекта исследований [6]


А) тополь пирамидальный Б) клён остролистный
Рис. 2. Исследуемые рядовые посадки насаждений вдоль Шахтинского шоссе
Таблица 1
Данные измерения диаметра клёна остролистного (AcerplatanoidesL.)на высоте 1,3 м (d1,3, см)
|
51,8 22,8 39,5 36,9 41,2 39,2 28,0 21,3 21,3 43,6 |
39,0 22,3 29,6 19,4 25,8 26,4 35,7 34,1 32,5 23,6 |
30,4 34,4 39,5 45,5 37,3 47,8 29,6 24,2 28,7 23,9 |
43,9 16,2 32,8 32,5 43,6 23,2 35,7 41,7 32,5 16,9 |
27,1 43,0 30,9 32,5 22,0 33,8 34,2 22,3 27,1 27,4 |
22,9 19,1 43,0 15,9 14,6 13,7 24,5 30,3 34,7 22,3 |
23,9 22,6 17,8 17,8 21,0 42,4 44,9 32,5 20,4 23,2 |
26,8 21,7 22,0 20,4 22,0 22,3 15,3 17,2 32,5 22,5 |
17,2 26,1 13,1 8,9 15,6 31,1 12,1 36,3 21,0 15,0 |
11,1 16,6 20,4 22,6 21,0 10,2 22,9 26,4 18,8 13,1 |
а) Все данные по диаметру надо разбить на k интервалов одинаковой длины, это необходимо для выполнения сводки данных наблюдения за измерением деревьев по диаметру. По приближенной формуле Стерджесса определяемчисло интервалов:
(1)
где - объём выборки. Число интервалов округляем до целого числа.
Длина интервала:
(2)
где - наибольший элемент выборки;
- наименьший элемент выборки.
Вычислим длину интервала:
(см).
(см)
Границы интервалов можно рассчитатьпо следующей формуле:
(3)
б) Сводку данных наблюдений выполняем с помощью ППП Mathcad.Интервальный ряд распределения частот, полученный по сводке данных наблюдения, представлен в виде таблицы 2.Ряд распределения (статистический рядраспределения частот) содержащий значения вариант, представляющих собой величины середин каждого интервала и соответствующих им частот представлен втаблице 3 и в таблице 4 – ряд распределения относительных частот.
в) Для построения гистограммы относительных частот необходимо знать длины интервалов (основания прямоугольников) и высоты
(плотность относительной частоты), ряд распределения плотности относительной частотыпредставлен в таблице 5.На рисунке 3 представлена гистограмма относительных частот.
Таблица 2
Интервальный ряд распределения частот
|
Интервалы |
8,9–14,3 |
14,3–19,7 |
19,7–25,1 |
25,1–30,5 |
30,5–35,9 |
35,9–41,3 |
41,3–46,7 |
46,7–52,1 |
|
Частота |
7 |
15 |
29 |
14 |
16 |
8 |
9 |
2 |
Таблица 3
Статистический ряд распределения частот
|
Значение |
11.6 |
17 |
22.4 |
27.8 |
33.2 |
38.6 |
44 |
49.4 |
|
Частота |
7 |
15 |
29 |
14 |
16 |
8 |
9 |
2 |
Таблица 4
Ряд распределения относительных частот
|
Значение |
11.6 |
17 |
22.4 |
27.8 |
33.2 |
38.6 |
44 |
49.4 |
|
Относительная частота
|
0.07 |
0.15 |
0.29 |
0.14 |
0.16 |
0.08 |
0.09 |
0.02 |
Таблица 5
Ряд распределения плотности относительной частоты
|
Значение |
11.6 |
17 |
22.4 |
27.8 |
33.2 |
38.6 |
44 |
49.4 |
|
Плотность |
0.013 |
0.028 |
0.054 |
0.026 |
0.03 |
0.015 |
0.017 |
0.0037 |
Рис. 3. Полигон и гистограмма относительных частот. Теоретическая кривая нормального распределениядиаметровклёна остролистного (AcerplatanoidesL.) на высоте 1,3 м
Соединяя середины верхних сторон прямоугольников отрезками прямых линий, получаем полигон относительных частот (ломаная линия). По виду гистограммы (полигона) рисунка 3выдвигаем гипотезу о нормальном распределении признака Х – измерение диаметров клёна остролистного (AcerplatanoidesL.)на высоте 1,3 м (d1,3, см).
г) Основные статистические показатели вычислим с помощью ППП Mathcad.
Так как следовательно, изменчивость данного признака (диаметра клёна)является значительной.Так как А>0, то асимметрия – левосторонняя, потому что вершина полигона сдвинута влево относительно вершины кривой нормального распределения (пунктирная линия на рисунке 3). Эксцесс Е<0, это говорит о том, чтолиния распределения вариант данного ряда проходит ниже кривой нормального распределения.
д)Далее вычислим ошибки среднего выборочного значения, среднего квадратичного отклонения, коэффициентов вариации (%), асимметрии и эксцесса:
Путём вычисления отношения величины рассматриваемого показателя к его ошибке рассчитывается оценка достоверности показателей:
Полученные показатели достоверности сравниваем со стандартной величиной критерия Стьюдента t(k, ), при числе степеней свободы k=n–1=100–1=99(n =100) и уровне значимости
.Значения показателей достоверности для выборочной средней, среднего квадратичного отклонения, коэффициента вариации и асимметрии больше, чем
, то перечисленные статистические показатели достоверны на 5%-ном уровне значимости. Значение показателя достоверности для эксцесса меньше, чем
, следовательно, эксцесс недостоверны на 5%-ном уровне значимости, что видно и на рисунке, 3.
е)По критерию Пирсона (при заданном уровне значимости ) проверим гипотезу о нормальном распределении генеральной совокупности. Для этого необходимо найти теоретические частоты
с помощью формулы плотности нормального распределения:
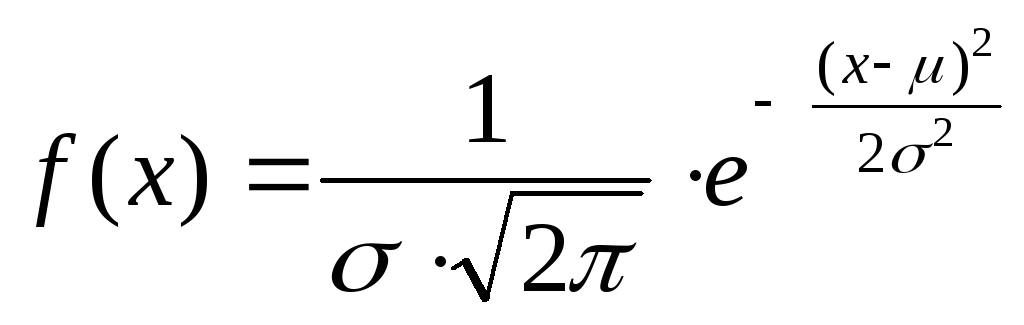 , (4)
, (4)
где - выборочное среднее, σ – среднее квадратическое отклонение;
Тогда :
, (5)
Затем, с помощью критерия Пирсона сравним эмпирические ( ) и теоретические (
) частоты:
По таблице критических точек распределения с заданным уровнем значимости
и числу степеней свободы
находим критическую точку правосторонней критической области
. Так как
, то гипотезу о нормальном распределении генеральной совокупности отвергаем.
Аналогично, с помощью данной программы, можно провести статистическую обработку и других данных с пробной площади из инвентаризационной ведомости (высоты деревьев (h, м), диаметра на высоте
Проведённые исследования (расчёты)с использованием ППП Mathcadпозволяют вывести следующие результаты, дать практические рекомендации и выводы.
Результаты анализа данной выборки диаметров клёна остролистного (AcerplatanoidesL.) на высоте 1,3 м:
– выборочная средняя измерений деревьев по диаметру составляет 27,1 см;
– изменчивость диаметра клёна остролистного характеризуется средним квадратическим отклонением, которое для выборочной совокупности составляет см, коэффициент вариации равен
, что говорит о значительной изменчивости деревьев по диаметру и подтверждается опытными данными. Проанализировав интервальный ряд распределения выборки, видим, что для улучшения полученных результатов можно отбросить нехарактерные данные, т.е. последний интервал (таблица 2), объединить с предпоследними, что позволит уменьшить среднее квадратическоеотклонение и коэффициент вариации. Диаметр у деревьев клёна, посаженных в один вегетационный период сильно варьируется, возможно, это связано с климатическими условиями, приживаемостью деревьев и другими факторами, которые влияют на рост и развитие насаждений;
– оценка достоверности основных статистических показателей приводит к выводу о надёжности выборочной средней, среднего квадратическогоотклонения, коэффициента вариации и асимметрии на 5%-ном уровне значимости. В то же время такой показатель, как эксцесс, характеризующий крутость эмпирической кривой, недостоверен, что позволяет считать его практически отсутствующим;
– на основании проверки критерия согласия Пирсона мы приходим к выводу о том, что измерения деревьев по диаметру нельзя считать распределенными по нормальному закону. Это можно объяснить недостаточным объёмом выборки и наличием нехарактерных показателей.
Главные выводы проделанной работыс использованием ППП Mathcadсостоят в том, что были показаны последовательные и подробные этапы математической обработки результатов лесокультурных исследований, расчёт основных статистических показателей (выборочная средняя измерений деревьев по диаметру, выборочная дисперсия, среднее квадратическое отклонение, коэффициент вариации иасимметрии на 5%-ном уровне значимости) и их оценка (оценка достоверности основных статистических показателей). ППП Mathcadпозволяет оперировать большим числом данных, быстро и с достаточной точностью обрабатывать и сравнивать результаты измерений,полученных при подеревной инвентаризации в лесном хозяйстве, поэтому данную программу можно внедрять в производство, в работе на конкретных примерах пошагово представили действия и расчёты для получения основных статистических показателей, применительно к лесокультурным исследованиям.
1. Baryshnikova, E.V. Matematika. Matematicheskaya statistika [Tekst]: metod. ukazaniya k vypolneniyu raschetno-graficheskoy raboty dlya studentov vseh special'nostey / E.V.Baryshnikova; Fed. gos. byudzhetnoe obrazovat. uchrezhdenie vyssh. prof. obrazovaniya «Novocherkasskaya gos. melior. akad.», kaf. matematiki.- Novocherkassk, 2010.- 61 s.
2. Gmurman, V.E. Teoriya veroyatnostey i matematicheskaya statistika: ucheb. posobie dlya vuzov [Tekst]: ucheb. posobie dlya vuzov- 9-e izd., ster. Knigi Matematika /V.E. Gmurman.- M.: Vysshaya shkola, 2003. - 479 s. EDN: https://elibrary.ru/QJLKXP
3. GOST 16483.6-80 (ST SEV 1141-78). Drevesina. Metod otbora model'nyh derev'ev i kryazhey dlya opredeleniya fiziko-mehanicheskih svoystv drevesiny nasazhdeniy. - Vved. 1981-01-01 [Tekst]. - M.: Standartinform, 2005. - 6 s.
4. Dospehov, B. A. Metodika polevogo opyta (s osnovami statisticheskoy obrabotki rezul'tatov issledovaniy) [Tekst] / B.A. Dospehov. - 5-e izd., dop. i pererab. - M.: Agropromizdat, 1985. - 351 s., il.
5. Zaycev, G.N. Matematicheskaya statistika v eksperimental'noy botanike [tekst] / G.N. Zaycev. - M.: Izd. Nauka, 1984. - 424 s.
6. Ivonin, V.M. Lesomelioraciya landshaftov.Nauchnye issledovaniya [tekst] / V.M. Ivonin, N.D. Pen'kovskiy. - Rostov-na-Donu, 2003. - 152 s.
7. Karta g. Novocherkasska (Shahtinskoe shosse) [Elektronnyy resurs]. - rezhim dostupa: https://www.google.com/maps/@47.5039335,40.1025466,1514m/data=!3m1!1e3?hl=ru-RU. - Zagl. s ekrana.
8. Koh, E.V. Vertikal'naya struktura fitomassy v sosnyakah iskusstvennogo proishozhdeniya [Tekst]: avtoref. … kand. s.-h. nauk: 06.03.02/ E.V. Koh. - Ekaterinburg, 2013. - 24s. EDN: https://elibrary.ru/SVCYZJ
9. Kochegurova, E.A. Osnovy raboty i programmirovaniya v sisteme Mathcad [Tekst]: ucheb. posobie / E.A. Kochegurova. -Tomsk, 2012. - 25 s.
10. Kruzhilin, S.N. Rost duba chereshchatogo v lesnyh kul'turah, sozdannyh s primeneniem raznyh tipov smesheniya v usloviyah Nizhnego Dona [Tekst]: avtoref. … kand. s.-h. nauk: 06.03.01/ S.N. Kruzhilin. - Bryansk, 2008. - 25s. EDN: https://elibrary.ru/NJJIBJ
11. Medvedeva, E.Yu. Biologo-ekologicheskie osobennosti rosta i razmnozheniya gibridnyh topoley v gorode Ekaterinburge [Tekst]: dis. … kand. s.-h. nauk: 06.03.03: zaschischena 07.10.2015 / E.Yu. Medvedeva. - Ekaterinburg, 2015. - 210 s. - Bibliogr.: s. 166-187. EDN: https://elibrary.ru/EORHYK
12. Mitropol'skiy, A.K. Tehnika statisticheskih vychisleniy [Tekst]: 2-e izd., pererab. i dop. seriya «Fiziko-matematicheskaya biblioteka inzhenera» /A.K. Mitropol'skiy. - M.: Nauka, 1971. - 576 s. : il.
13. Prikaz Ministerstva obrazovaniya i nauki Rossiyskoy Federacii №1027 ot 23 oktyabrya 2017 goda (red. ot 23.03.2018) «Ob utverzhdenii nomenklatury special'nostey, po kotorym prisuzhdayutsya uchenye stepeni» [Elektronnyy resurs] // informacionno-pravovoy portal GARANT.RU. - Rezhim dostupa: https://www.garant.ru/products/ipo/prime/doc/71714408/.
14. Tanyukevich,V.V. Ekologo-meliorativnoe sostoyanie osokornikov v usloviyah zagryazneniya Dono-Aksayskoy poymy [Tekst]: dis. ... kand. s.-h. nauk: 03.00.16: zaschischena 10.12.2004 / V.V. Tanyukevich. - Novocherkassk, 2004. - 225 c. - Bibliogr.: s 182-201. EDN: https://elibrary.ru/NMYAVT
15. Knibbeler, V.•Higher-Dimensional Automorphic Lie Algebras Lombardo [Text] / V. Knibbeler, S.•Lombardo, Jan A. Sanders // The Journal of the Society for the Foundations of Computational Mathematics. - 2017. - Vol. 17, no4. - pp. 987-1035. DOIhttps://doi.org/10.1007/s10208-016-9312-1. EDN: https://elibrary.ru/TVGNUE
16. McNeill,J.Major changes to the Code of Nomenclature - Melbourne, July 2011[Text] / J. McNeill, N.J. Turland // Taxon. -2011. -Vol. 60, no. 4 - pp. 1495-1497.
17. Pearsall, D.M. Encyclopedia of Archaeology[Text] / D.M. Pearsall. - San Diego, Calif. : ElsevierAcademic Press, 2008. - 2382 p. EDN: https://elibrary.ru/QPRAIN
18. Warne, R. Statistical Methods Used in Gifted Education Journals, 2006-2010 [Text] / R. Warne, M. Lazo, T. Ramos, and N. Ritter // Gifted Child Quarterly. -2012. - Vol. 56, no 3. - pp. 134-149. doi:https://doi.org/10.1177/0016986212444122.
19. White, C. Unkind cuts at statisticians [Text] / C. White //The American Statistician. - 1964. - Vol. 18, no. 5. - pp. 15-17.












